别着急,坐和放宽
原数组: 前缀和: 差分:
一维前缀和
构建
快速求$[l,r]$ 的和
二维前缀和
img
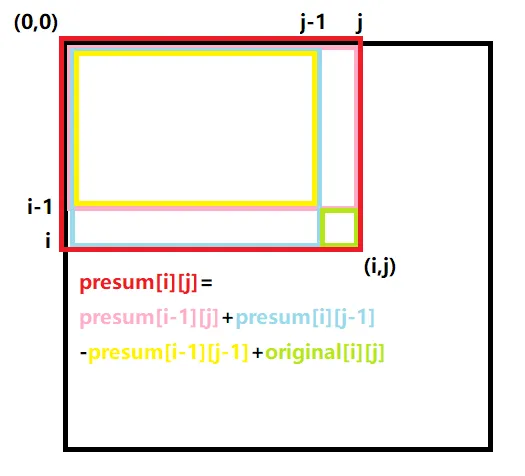
类比一维的情形,$S{i,j}$ 应该可以基于 $S{i-1,j}$ 或 计算,从而避免重复计算前面若干项的和。但是,如果直接将 和 相加,再加上 ,会导致重复计算 这一重叠部分的前缀和,所以还需要再将这部分减掉。
在已经预处理出二维前缀和后,要查询左上角为 、右下角为 的子矩阵的和,可以计算
这可以在 时间内完成
在二维的情形,以上算法的时间复杂度可以简单认为是 ,即与给定数组的大小成线性关系。但是,当维度 增大时,由于容斥原理涉及的项数以指数级的速度增长,时间复杂度会成为 ,其中 是数组维度,而 是给定数组大小。因此,该算法不再适用。
一维差分
img
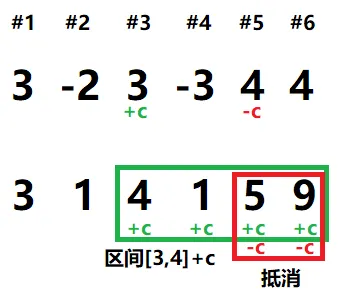
对于序列 ,它的差分序列 是指
构造与修改可以统一
insert(i,i,a[i]);
insert(l,r,c);
给区间 中每个数 :
$$
\begin{align}
b[l]\ &+!=c\
b[r+1]\ &-!=c
\end{align}
$$
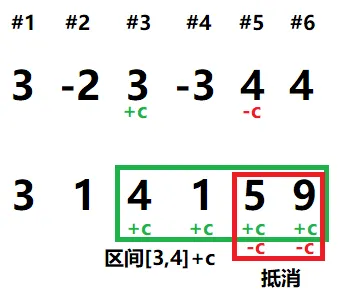
在所有修改操作结束后,可以通过前缀和操作恢复更新后的 的值。单次修改是 的。查询时,需要做一次 的前缀和操作,随后每次查询都是 的。
二维差分
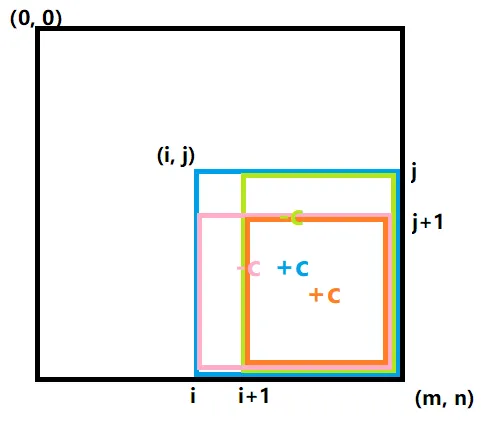
img
CodeBlock Loading...
CodeBlock Loading...