基础算法-总览
数据结构
在解决问题的时候,我们通常不是一下子把数据处理完,更多的时候需要先把它们放在一个容器里,等到一定的时刻再把它们拿出来。使用「数据结构」是一种「空间换时间」思想的体现,
| 数据结构 | 应用场景 |
|---|---|
| 栈 | 符合「后进先出」的规律 |
| 队列 | 符合「先进先出」的规律 |
| 哈希表(散列表) | 实现「快速存取」数据的功能 |
| 二分搜索树(红黑树、B 树系列) | 维护了一组数据的顺序性,得到一个数据的上下界 |
| 并查集 | 用于处理不相交集合的「动态」连接问题 |
| 优先队列 | 有「动态」添加、删除数据且需要获得最值的场景 |
| 字典树(Trie) | 用于保存和统计大量的字符串和相关的信息 |
| 线段树 | 处理数组的区间信息的汇总(求和、最值等)、单点更新、区间更新问题 |
| 树状数组 | 处理数组的前缀和、单点更新、区间更新问题 |
时间复杂度与空间复杂度
g(N) 关于规模 N 的表达式
O(g(N)) 表达考虑最坏情况
时间复杂度的计算(估算)只有在输入规模特别大的时候才有意义。「输入规模特别大」往往是我们初学的时候不可感知的。大 𝑂表示法是一种事前估计法,得到一个函数表达式,它表示了:随着输入规模的扩大,程序的执行消耗会扩大的程度。这个程度不是直接从表达式上直接看出来的,需要在一个动态增加的过程中去理解程序的执行消耗会扩大的程度。
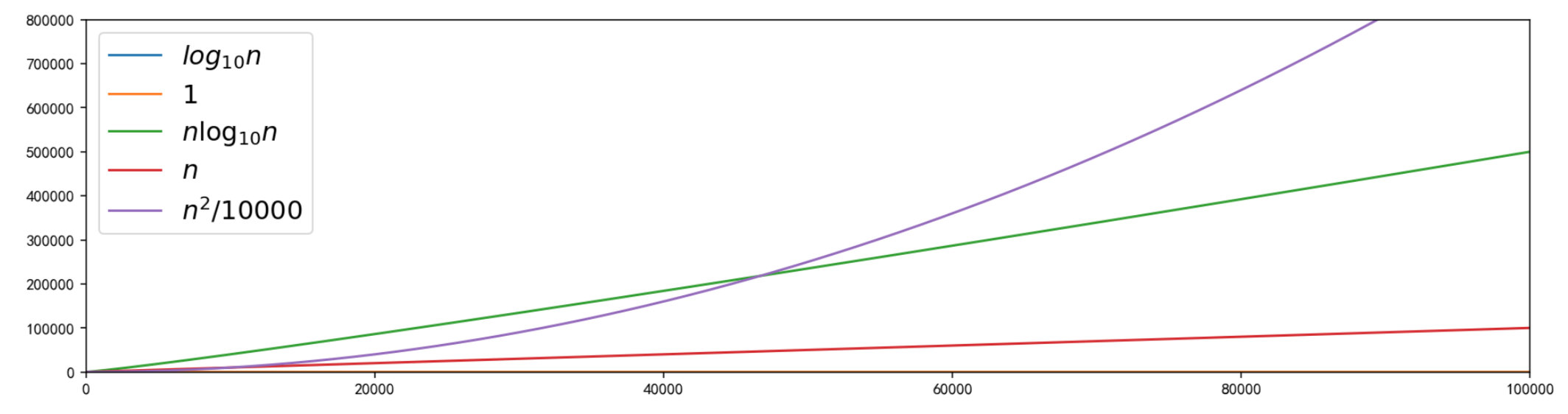
t1
这个函数的图形随着 𝑛的成倍增长,纵轴数值的增长较缓慢(这已经是一种很好的时间复杂度了),到了 100000这个数量级,函数值也才到 5,「二分查找」就具有这样的时间复杂度:随着输入数据规模的增加,函数的执行次数增长较缓慢
的函数图像表示了程序的运行时间与输入数据的规模无关;
随着的成倍增长,函数值也成比例地增长,这样的时间复杂度是性能相对较差的,这样的算法常常是「朴素解法」和「暴力解法」
在 50000 以后 有着更高算法复杂度。

t2
参考学习:力扣
其他知识补盲
三元运算符
条件表达式 ? 表达式1 : 表达式2
意思是:
- 如果 条件表达式为真(即非 0),结果就是 表达式1;
- 否则,结果就是 表达式2。
它相当于一个简写版的 if...else...。
printf 控制小数输出
printf("%.nf", x);
%f:输出浮点数(float / double)%.n:表示保留 n 位小数,会四舍五入- 输出宽度(可选):
%m.nf→ 总宽度 m,小数 n
double x = 3.14159;
printf("%.2f\n", x); // 输出:3.14
printf("%.3f\n", x); // 输出:3.142
printf("%8.2f\n", x); // 输出: 3.14 (总宽8位,右对齐)
- 只显示指定的小数位(四舍五入)
- 不自动切换科学计数法
- 精确控制格式,非常适合输出表格或文件格式数据
cout 控制小数输出
#include <iomanip>
| 控制符 | 作用 |
|---|---|
setprecision(n) | 设置有效数字个数(默认)或小数位数(配合 fixed) |
fixed | 改变 setprecision 的含义:表示小数点后位数 |
scientific | 科学计数法输出 |
showpoint | 强制显示小数点与小数 |
setw(n) | 设置最小输出宽度 |
setfill(c) | 设置填充字符 |
例 1:默认行为(有效数字)
double x = 3.14159;
cout << setprecision(3) << x; // 输出:3.14(有效数字3位)
解释:默认模式下,setprecision 控制有效数字,而不是小数点后几位。
例 2:保留小数位数(配合 fixed)
cout << fixed << setprecision(3) << x; // 输出:3.142
解释:fixed 改变了 setprecision 的含义,使它控制“小数点后几位”。
例 3:科学计数法
cout << scientific << setprecision(2) << x;
// 输出:3.14e+00
例 4:组合使用
cout << setw(8) << setfill('*') << fixed << setprecision(2) << x;
// 输出:***3.14
比较:printf vs. cout
| 功能 | printf | cout |
|---|---|---|
| 输出小数位 | %.2f | fixed << setprecision(2) |
| 输出有效数字 | %.2g | setprecision(2)(默认) |
| 科学计数法 | %.2e | scientific << setprecision(2) |
| 显示小数点 | %#.f | showpoint |
| 输出宽度 | %8.2f | setw(8) |
| 需求 | printf 写法 | cout 写法 |
|---|---|---|
| 保留 2 位小数 | printf("%.2f", x); | cout << fixed << setprecision(2) << x; |
| 输出 3 位有效数字 | printf("%.3g", x); | cout << setprecision(3) << x; |
| 科学计数法 | printf("%.3e", x); | cout << scientific << setprecision(3) << x; |
| 输出宽度 8,小数 2 位 | printf("%8.2f", x); | cout << setw(8) << fixed << setprecision(2) << x; |
ACM数据类型选择
一、整型类型选择
| 类型 | 字节数(C++标准) | 取值范围 | 常用场景 |
|---|---|---|---|
int | 4字节 | ±2,147,483,647 ≈ ±2×10⁹ | 普通下标、计数器、循环变量 |
long long | 8字节 | ±9,223,372,036,854,775,807 ≈ ±9×10¹⁸ | 大整数范围计算(如10¹², 10¹⁵) |
unsigned long long | 8字节 | 0 ~ 1.8×10¹⁹ | 非负大数、位运算、哈希、组合数模运算 |
| 数据范围 | 推荐类型 | 举例 |
|---|---|---|
| ≤10⁹ | int | n ≤ 10⁸,数组大小、索引 |
| ≤10¹² | long long | n² 或和的累计,∑a[i] |
| ≤10¹⁸ | long long | 涉及乘法、阶乘近似、模运算 |
| >10¹⁸ | __int128 | 大整数乘除、斐波那契巨大项 |
注意乘法溢出
如果题中:
a、b都 ≤ 10⁹- 但出现
a * b那么a * b可能达 10¹⁸,要 提前转 long long。
大整数取模
使用unsigned long long刚好多那一点就能确保long long数据能被取模了
二、浮点类型选择
| 类型 | 字节数 | 有效数字位数 | 常见误差 | 常用场景 |
|---|---|---|---|---|
float | 4字节 | 约6位有效数字 | 误差较大 | 一般不用 |
double | 8字节 | 约15位有效数字 | 10⁻¹⁵ | 主力 |
long double | 16字节(部分编译器) | 约18~19位 | 更高精度但慢 | 高精度几何、概率、积分题 |
浮点类型选取规则
| 精度需求 / 数据范围 | 推荐类型 | 举例 |
|---|---|---|
| 1e-3 或输出 2~3 位小数 | double | 平均数、几何长度 |
| 高精度计算(误差 < 1e-9) | double | All |
| 极端精度(1e-15 以内) | long double | 几何交点、积分、牛顿迭代 |
| 无需浮点,能整算 | 用 long long 代替 | 避免精度误差 |
浮点比较时不要用 ==,而是:
if (fabs(a - b) < 1e-9)
三、实际题目举例
| 题目数据范围 | 推荐类型 | 说明 |
|---|---|---|
| n ≤ 10⁵,aᵢ ≤ 10⁹ | long long | 可能求和到 10¹⁴ |
| n ≤ 10⁶,aᵢ ≤ 10⁶ | int | 总和 10¹² 仍安全在 long long |
| 坐标 ≤ 1e6,有平方根或几何距离 | double | 因为要开根号 sqrt |
| 坐标 ≤ 1e9,要计算角度或面积 | long double | 防止误差积累 |
| 模数 1e9+7, 998244353 | long long | 模乘必须防止溢出 |
| 阶乘 / 组合数 / 大数幂 | long long 或 __int128 | 有乘法放大 |
四、__int128 的应用
当题中要求:
- 计算
a*b,而a,b都可能到 1e18; - 或
(a*b)%mod中a*b可能溢出long long;
可以使用:
__int128 mul(__int128 a, __int128 b, long long mod) {
return (a * b) % mod;
}
输出时要手动转换:
void print(__int128 x) {
if (x == 0) return;
print(x / 10);
putchar(x % 10 + '0');
}
| 场景 | 建议 |
|---|---|
一律使用 long long 存整数,除非确定不会溢出 | 防止隐藏错误 |
所有浮点题默认用 double | 兼顾精度与速度 |
| 输出时明确格式控制 | setprecision 或 printf("%.6f") |
| 出现“平方”、“乘积”、“累积和”关键字时立刻提升精度 | 经验法则 |
| 模数题(1e9+7, 998244353) | 仍用 long long |
| 几何题或误差题 | double / long double + eps 比较 |
读入速度相关
| 数据规模(输入量级) | 做法 | 原因 |
|---|---|---|
| ≤ 1×10⁵ | 普通 cin >>、cout << 即可 | - |
| 1×10⁵ ~ 5×10⁵ | 关闭同步流(ios::sync_with_stdio(false); cin.tie(nullptr);) | 提升约 2~3 倍性能 |
| 5×10⁵ ~ 2×10⁶ | 使用 scanf/printf 或快读模板 | cin 可能开始卡 |
| ≥ 2×10⁶ | 必须使用快读 | TLE |
| 题型 | 通常输入量 | 是否要优化 |
|---|---|---|
| 普通数据结构、数学题 | ≤ 1e5 | 否 |
| 排序、扫描、模拟 | 1e5~1e6 | 关闭同步流 |
| 离散化、前缀和、差分 | 1e6 | 使用快读 |
| 大规模统计、字符串处理 | ≥ 1e6 | 必须快读 |
快读板子
#define rd read()
inline long long read()
{
long long x = 0, y = 1;
char c = getchar();
while (c > '9' || c < '0')
{
if (c == '-')
y = -1;
c = getchar();
}
while (c >= '0' && c <= '9')
x = x * 10 + c - '0', c = getchar();
return x * y;
}
//使用long long n = rd;
字符处理相关
字符与整数的相互转换
| 表达式 | 含义 | 示例 |
|---|---|---|
'a' | 字符常量(ASCII 值为 97) | 'a' + 1 → 'b' |
s[i] - 'a' | 把小写字母映射到 0~25 | 'a' - 'a' = 0, 'z' - 'a' = 25 |
(unsigned char)s[i] | 把字符安全地转为无符号整数,防止负值 | 常用于 cnt[(unsigned char)s[i]]++ |
(int)s[i] | 查看字符对应的整数(ASCII) | 'A' → 65, 'a' → 97 |
string s = "abc";
int num[26] = {0};
for (char c : s)
num[c - 'a']++; // 统计字母出现次数
int cnt[256] = {0};
for (unsigned char c : s)
cnt[c]++; // 统计所有 ASCII 字符出现次数
字符串输入相关语法
| 用法 | 功能 | 特点 |
|---|---|---|
cin >> s; | 输入一个字符串(自动跳过空格、换行) | 读到空格或换行就停 |
getline(cin, s); | 输入整行(包括空格) | 读到换行符才停 |
cin.getline(c, n); | 读取一整行到 C 风格字符数组中 | c 是 char[],会自动加上 '\0' 结尾 |
getchar(); | 读取一个字符 | 常用于“吃掉”换行符或分隔符 |
cin.get(); | 同样读取一个字符(可读空格) | 返回类型是 int(EOF 安全) |
注意 cin 和 getline 混用问题
当用过 cin >> n; 之后,缓冲区里 还残留一个换行符 '\n'。
如果立刻用 getline(cin, s),那它会把这个换行符当作空行。
所以需要:
cin >> n;
getchar(); // 或 cin.ignore();
getline(cin, s); // 现在才能正确读入整行
C 风格输入输出(scanf / printf)
| 函数 | 功能 | 特点 |
|---|---|---|
scanf("%d", &n); | 输入一个整数 | 快,但格式严格 |
scanf("%s", str); | 读取一个不含空格的字符串 | 自动加 \0 |
scanf("%[^\n]", str); | 读取整行直到换行 | 注意需要清理缓冲区 |
printf("%d", n); | 输出整数 | 格式控制灵活 |
getchar() | 从标准输入读取一个字符 | 常用于吸收换行符 |
常见字符串处理操作
| 操作 | 语法 | 含义 |
|---|---|---|
| 获取长度 | s.size() 或 s.length() | 返回字符个数 |
| 访问字符 | s[i] | 第 i 个字符(0 起) |
| 拼接 | s += t; | 拼接字符串 |
| 截取 | s.substr(pos, len) | 从 pos 开始取 len 个字符 |
| 查找 | s.find("abc") | 找到返回位置,否则返回 string::npos |
| 转数字 | stoi(s) | 字符串 → 整数 |
| 转字符串 | to_string(x) | 整数 → 字符串 |
| 类别 | 示例 | 说明 |
|---|---|---|
| 字符统计 | cnt[(unsigned char)s[i]]++ | 防止负下标 |
| 字符映射 | num[s[i] - 'a'] | 字母映射到数组索引 |
| 输入整行 | getline(cin, s) | 包含空格 |
| 吸收换行 | getchar() / cin.ignore() | 避免 getline 读空行 |
| C风格行读入 | cin.getline(c, n+1) | 填充 char[] |
| 判断类型 | isalpha, isdigit, … | 判断字符类型 |
| 转换 | toupper, tolower | 大小写转换 |